Solve a Substitution Cipher with a Markov chain

There are k! substitution ciphers for an alphabet with k letters—too many for an exhaustive search. With a frequency-based approach adapted to the graph of alphabetic ciphers, we redefine the act of deciphering as a sampling problem suitable for a Metropolis-Hastings random walk. A substitution cipher is thus solvable with a Markov chain.

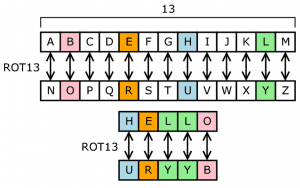
Let’s begin with a review of some basic cryptography: a simple substitution cipher replaces letters one-for-one in the target language. There are thus $26!$ possible English substitution ciphers.

Brute force

Caesar cipher image, demonstrating graphic base for substitution cipher by markov chain

With the set of all ciphers

$\Omega={(a_1,a_2,\ldots,a_n)}\,,$

we shuffle through $\Omega$ by reassignment of letters in a guess $G$ ,

$G: (a,b,c,\ldots, z) \mapsto (x_1, \ldots, x_{26})\,.$

One way of reassignment is by rotation as with the Caesar cipher.

For a brute force tactic the objective is to overwhelm the solution space. With $O(k!) = 26!$ possible English substitution ciphers this is unfeasible, so we turn to methods such as frequency analysis to make educated guesses.

Assign keys to letters—evaluate, and repeat until a pattern emerges from the yet-to-be decrypted text.

Scoring a Key

We can evaluate a cipherkey’s fitness by comparing the distributions of letter and letter-to-letter frequencies. If we swap two letter assignments, the change in fitness is measured as a difference between corresponding frequency tensors.

To do so efficiently, we swap the corresponding row/column pairs and recompute only the impacted entries.

First order frequency matrix

The first-order frequency tensor is a matrix. For the letter ‘a’ it measures the distribution of letters ‘a’–’z’ that come after it. This is equivalent to counting occurrences of digrams ‘aa,’ ‘ab,’ … , ‘az’ in the cipher text.

The evaluated ciphertext is compared against a baseline: assuming we’re tracking the first-order letter-to-letter frequencies, we obtain the frequency tensor by counting the digrams in a known English text. By comparing the digrams, we form a statistical foundation to solve the substitution cipher by Markov chain. A score is obtained as the cumulative difference between entries in both tensors.

Statistical Objective Function

By comparing scores, obtained from values representing frequencies, we construct the $\chi^2$ test from Statistics. Define

$\phi(\bold x) = \text{score} := \sum_{i\in I}\frac{(x_i - \mu_i)^2}{\mu_i} \sim \chi^2$

for the first-order frequencies $I=\{f(aa), f(ab), f(ac), \ldots, f(zz)\}$ and English baseline $\mu_i$ .

The solution to the cipher is the $x \in \Omega$ providing lowest discrepancy $\phi(x)$ from the baseline distribution of digram frequencies.

Global Optimization

In general, the solution key to a ciphertext provides a global optimum to the score function $\phi$ . If we were to choose a strict optimizer, and choose new cipher-letter assignments on a strict basis of improving the score $\phi(\bold x)$ over some initial guess $\bold x_0$ , we would soon be trapped at one of many the many local optima to $\phi$ . This task is thus ill-posed for hill-climb-like methods.

Instead we must allow our attempted solution to degrade at times—balancing exploration of the solution space with optimization of the score.

Bottlenecks

black and white round tunnel is like a bottleneck for solving substitution cipher by markov chain

Solving a cipher one letter-swap at a time, 25/26 letters of the alphabet must be nailed down before we’re able to identify all 26.

In order to get to the appropriate solution, we must pass through certain regions, known as bottlenecks.

A strict optimizer has a hard time passing through the bottleneck. In scoring text, ehllo $\approx$ elhho $\neq$ hello, so we become trapped at a local optimum. Solving a substitution cipher by Markov chain means we end up cycling between the best nearby solutions.

One way to do this is with a Metropolis-Hastings (MH) algorithm.

Sampling with Metropolis-Hastings

$x_0 \longrightarrow x$

Suppose we want to sample from the stationary i.e. asymptotic distribution $P$ of an ergodic Markov chain.

From the Markov balance equation

$P(x|x_0)P(x_0) = P(x_0|x)P(x)$

define the probability $A$ we accept a new state $x$ by the proportion

$\frac{A(x|x_0)}{A(x_0|x)} = \frac{P(x)}{P(x_0)} \frac{g(x_0|x)}{g(x|x_0)}$

Here, $g$ can be any function assigning nonzero values to all states $x$ .

$g$ is known as the proposal distribution, and is chosen with a specific problem in mind. For Metropolis-Hastings as a sampling method, $g$ should be chosen to minimize the impact of starting guess $x_0$ i.e. reduce the chain’s mixing time.

We will apply the Metropolis-Hastings algorithm to sample from the set of cipherkeys with good score. In particular, we’d like to compute the unique sample argmin $_{\bold x} \phi(\bold x)$ . Using MH, we select new cipherkeys randomly, but with a configurable bias toward improvements in score.

Proposing a Key

Denoting $x_0,x_1,\ldots, x_k$ the cipherkeys we will have guessed in $k$ steps of our algorithm, define the probability $A$ that we accept a new cipherkey. In the case of blindly choosing any one of the $26!$ keys with equal probability, we are sampling from a uniform stationary distribution of cipher keys

$P(x|x_0) = 1/26!$

accepting any new keys with relative probabilities

$\frac{A(x|x_0)}{A(x_0|x)} = \frac{P(x)}{P(x_0)} \frac{g(x_0|x)}{g(x|x_0)} = \frac{1}{1} \frac{g(x_0|x)}{g(x|x_0)} = 1$

where $g(x|x_0) = 1/26!$ for any current key $x_0$ and proposed $x$ .

Controlling the Optimization Rate

For something beyond brute force, however, we can use an Ising model. The Ising model assigns each key proposal a probability depending on differences in score

$\Delta\phi = \phi( x_t) - \phi ( x_{t-1})$

and a “temperature” $\lambda$ which we set aside as a free parameter of the optimization method. We accept a new key with probability

$\lambda^{\tanh(\Delta\phi) + 1}\,,\quad 0<\lambda\leq 1$

This produces a Metropolis-Hastings random optimizer that we can control through manipulating the Ising parameter $\lambda$ . When $\lambda \approx 0$ , we are strictly optimizing the score function $\phi$ , and when $\lambda \approx 1$ we are uniformly sampling all $26!$ cipherkeys.

The temperature $\lambda$ can be varied on the go. This is a fascinating analogue to metallurgical annealing, where metals such as bronze, tin, and copper are put through controlled fluctuations in temperature. The process of varying $\lambda$ over optimization is the focus of Simulated Annealing.

Github link